certidumbre: agosto 2012

martes, 7 de agosto de 2012

aplicaciones de uma transformacion lineal

En matemática una aplicación lineal (también llamada función lineal, transformación lineal u operador lineal) es una aplicación entre dos espacios vectoriales, que preserva las operaciones de suma de vectores y producto por un escalar.

En álgebra abstracta una aplicación lineal es un homomorfismo entre espacios vectoriales o en el lenguaje de la teoría de categorías un morfismo sobre la categoría de los espacios vectoriales sobre un

cuerpo dado.

Se denomina aplicación lineal, función lineal o transformación lineal a toda aplicación cuyo dominio y codominio sean espacios vectoriales que cumpla la siguiente definición:

Sean $V$ y $W$ espacios vectoriales sobre el mismo espacio o campo $K$ , y $T$ una función de $V$ en $W$ . $T$ es una transformación lineal si para todo par de vectores $u$ y $v$ pertenecientes a $V$ y para todo escalar $k$ perteneciente a $K$ , se satisface que:

$T(u+v) = T(u) + T(v) \,$
$T(ku) = kT(u) \,$ donde k es un escalar.

Transformación lineal identidad

$T:V \rarr V \quad/\quad T(x) = x,$ $\forall x \in V$

Homotecias

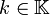
$T:\mathbb{K}^n \rarr \mathbb{K}^n \quad/\quad T(x) = kx$ con $k \in \mathbb{K}$

Si k > 1 se denominan dilataciones

Si k < 1 se denominan contracciones

Sea B = {v₁,v₂,v₃,...v_n} base de V y C = {w₁, w₂, w₃,...w_n} un conjunto de n vectores de W no necesariamente distintos, entonces existe una única transformación lineal T: V → W que satisface:

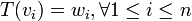
$T(v_i) = w_i, \forall 1\le i\le n$

Según la teoría de Brevis-Devaud, una matriz asociada es la matriz formada por las coordenadas de los elementos de una base.
Dada T: V → W, con B = {v₁, v₂, v₃, ..., v_n} y C = {w₁, w₂, w₃, ..., w_p} bases de V y W respectivamente, llamamos coordenadas de v₁ en base C, al vector formado por los coeficientes de los elementos de C que usamos para llegar al transformado de v₁.
T(v₁) = a₁.w₁ + a₂.w₂ + ... + a_p.w_p
Entonces:
coord_C(v₁) = (a₁, a₂,..., a_p)
Y la matriz asociada a T, en las bases B y C, es la matriz res/sub>(v₂), ..., coord_C(v_n))

TRANSFORMACION INVERSA

Sea X una variable aleatoria con función de distribución F_X(x).

Por resultados básicos de probabilidad, se tiene que U=F_X(X) es una variables aleatoria y sigue una distribución U(0,1). A continuación veremos un resultado recíproco. Previamente, establecemos la siguiente notación: dado $0\leq u \leq 1$ , se define

$\begin{displaymath}F_X^{-1}(u) = \min \{y \ / \ F_X(y)\geq u \}.\end{displaymath}$

Si $U\equiv U(0,1)$ y F es una función de distribución, entonces X=F^-1(U) tiene función de distribución F.
Demostración:
(i) Nótese en primer lugar que

$\begin{displaymath}F(F^{-1}(u)) = F( \text{mín} \{y \ / \ F(y) \geq u \} ) \geq u,\end{displaymath}$

$\begin{displaymath}F^{-1}(F(x))=\text{mín} \{y \ / \ F(y) \geq F(x) \} \leq x.\end{displaymath}$

(ii) Veamos que $\{ (u,x) \ / \ u\leq F(x)\}=\{(u,x) \ / \ F^{-1}(u) \leq x \}$ .
" $\subseteq$ " Sea (u,x) un elemento del primer conjunto.

$\begin{displaymath}u \leq F(x) \quad \rightarrow \quad F^{-1}(u)=\text{mín} \{y \ / \ F(y) \geq u \} \leq x .\end{displaymath}$

Luego (u,x) está en el segundo conjunto.

" $\supseteq$ " Sea ahora (u,x) un elemento del segundo conjunto.

$\begin{displaymath}F^{-1}(u) \leq x \quad \rightarrow \quad u \leq F(F^{-1}(u)) \leq F(x).\end{displaymath}$

Por lo tanto, (u,x) pertenece al primer conjunto.

(iii)

$\begin{displaymath}P(X\leq x) = P(F^{-1}(U)\leq x) = P(\{ (u,x) \ / \ F^{-1}(u)\leq x \}) =\end{displaymath}$

$\begin{displaymath}P(\{ (u,x) \ / \ u\leq F(x)\}) = P(U\leq F(x)) = F(x).\end{displaymath}$

La última igualdad por tratarse de una variable uniforme en el intervalo (0,1).

Q.E.D.

Así se tiene el siguiente método de la transformación inversa:

1.: Genérese u_i.
2.: Hágase x_i=F_X^-1(u_i).

Ejemplo: $X\equiv U(a,b)$

$\begin{displaymath}F_X(x)= \frac {x-a}{b-a}, \ x\in (a,b)\end{displaymath}$

$\begin{displaymath}\frac{x-a}{b-a}=u; \quad x-a=u(b-a); \quad x=a+(b-a)u\end{displaymath}$

Ejemplo: $X\equiv Exp(\lambda)$

$\begin{displaymath}F_X(x)=1-e^{-\lambda x}, \ x>0\end{displaymath}$

$\begin{displaymath}1-e^{-\lambda x} = u; \quad 1-u=e^{-\lambda x}; \quad x= - \frac{1}{\lambda} \ln (1-u).\end{displaymath}$

Ejemplo: $X_1,\dots,\ X_n$ variables aleatorias independientes con la misma función de distribución F_X y

$\begin{displaymath}X_{(n)}=\text{máx} \{X_1,\dots,\ X_n\}.\end{displaymath}$

$\begin{displaymath}F_{(n)}(x)=P(X_{(n)}\leq x)=P(X_1\leq x,\dots,\ X_n\leq x)= \end{displaymath}$

$\begin{displaymath}=\prod_{i=1}^n P(X_i\leq x) = F_X^n(x).\end{displaymath}$

$\begin{displaymath}F_X^n(x)=u\Rightarrow \quad x=F_X^{-1}(u^{\frac{1}{n}}).\end{displaymath}$

Sin embargo, este método presenta problemas cuando no es posible obtener F_X^-1 de forma explícita (por ejemplo, en la distribución normal).

matriz asociada de una transformacion lineales

Si bien las transformaciones lineales pueden estudiarse sin hacer referencia alguna a las bases de los espacios dominio y codominio, un cálculo efectivo de las mismas exige el conocimiento de dichas bases.

Cualquier transformación lineal T: V ® W puede representarse mediante una matriz: T(x) = A x. La matriz A dependerá de las bases elegidas para V y W. La matriz de una transformación lineal queda determinada cuando se conocen una base ordenada de V, una base ordenada de W y los transformados de la base de V, en la base de W.

Supongamos que el espacio V tiene una base {v₁, ..., v_n} y el espacio W tiene una base {w₁, ..., w_m}. Entonces cualquier transformación lineal de V en W se representa por una matriz A_{m x n}.

Si T (v_i) = a_i1 w₁ + .... + a_im w_m, entonces la columna i de A es (a_i1 .... a_im )^T

Ejemplos

ü Supongamos que en el plano x-y la transformación de matriz A lleva a cada vector a su reflejo tomando como espejo el eje x, y la transformación de matriz B lleva a cada vector a su simétrico respecto del origen. Encontrar las matrices A y B, usando como base de R² el conjunto {(1, 0), (0, 1)}.

a) ¿ Matriz A?

Transformado de (1, 0) = (1, 0)
Transformado de (0, 1) = (0, -1)

Entonces la matriz la matriz de la transformación es:

b) ¿ Matriz B?

Transformado de (1, 0) = (-1, 0)
Transformado de (0, 1) = (0, -1)

Entonces la matriz la matriz de la transformación es:

ü Encontrar A_3x5 asociada a la transformación lineal P₅ ® P₃ / T (P(t)) = d² P(t) /dt², transformando P₅ en P₃ (polinomios de grado ≤ 4 en polinomios de grado ≤ 2).

Base en P₅: {1, t, t², t³, t⁴}. Base en P₃: {1, t, t²}

     Transformado de (1, 0, 0, 0, 0) = ( 0, 0, 0)
     Transformado de (0, 1, 0, 0, 0) = ( 0, 0, 0)
     Transformado de (0, 0, 1, 0, 0) = ( 2, 0, 0)
     Transformado de (0, 0, 0, 1, 0) = ( 0, 6, 0)
     Transformado de (0, 0, 0, 0, 1) = ( 0, 0, 12)

Entonces la matriz la matriz de la transformación es:

radio y nucleo de una transformacion lineal

El núcleo de una transformación lineal está formado por el conjunto de todos los vectores del dominio que tienen por imagen al vector nulo del codominio.
Para la transformación lineal
:TR R→ definida por:

Obtener:
(a) El núcleo de T y su dimensión.
(b) El recorrido de T y su dimensión.

SOLUCIÓN:

Matriz canónica
escalonada
(a) • El núcleo está dado por el conjunto

• Se propone al vector

Dimensión
, cuya imagen es:

lunes, 6 de agosto de 2012

algebra de transformaciones llineales

Una transformación lineal es un conjunto de operaciones que se realizan sobre un vector para convertirlo en otro vector. En ocasiones trabajar con vectores es muy sencillo ya que pueden ser facilmente interpretados dentro de un contexto gráfico, lamentablemente no siempre ocurre y es necesario transformar a los vectores para poderlos trabajar más facilmente. Por otra parte, trabajar con sistemas lineales es mucho más sencillo que con sistemas no lineales, ya que se puede utilizar una técnica llamada superposición, la cual simplifica de gran manera gran variedad de cálculos, por lo que es de gran interes demostrar que un proceso puede ser reducido a un sistema lineal, lo cual solo puede lograrse demostrando que estas operaciones forman una transformación lineal.

Se denomina transformación lineal, función lineal o aplicación lineal a toda aplicación cuyo dominio y codominio sean espacios vectoriales y se cumplan las siguientes condiciones:

Sean

V

W

espacios vectoriales sobre el mismo campo

K

, y

T

una función de

V

W

T

es una transformación lineal si para cada par de vectores de

u

v

pertenecientes a

V

y para cada escalar

k

perteneciente a

K

, se satisface que:

$T(u+v) = T(u) + T(v) \,$
$T(ku) = kT(u) \,$ donde k es un escalar.
Son aplicaciones lineales los operadores usados en la formulación matemática de la mecánica cuántica. Para detalles específicos sobre estos, ver el artículo Operador (mecánica cuántica).

Propiedades de las transformaciones lineales

Transformación Lineal Singular y No Singular

Sean y espacios vectoriales sobre el mismo campo y una transformación lineal de en . Entonces, es no singular si:X
En caso contrario es singular.

Teorema fundamental de las transformaciones lineales

Sea B = {v₁,v₂,v₃,...v_n} base de V y C = {w₁, w₂, w₃,...w_n n} un conjunto de vectores de W no necesariamente distintos, entonces existe una única transformación lineal Para todo

Clasificación de las transformaciones lineales

Monomorfismo: Si es inyectiva, o sea si el único elemento del núcleo es el vector nulo.

Epimorfismo: Si es sobreyectiva (exhaustiva).
Isomorfismo: Si es biyectiva (inyectiva y exhaustiva).
Endomorfismo: Si o sea si el dominio es igual al codominio (el espacio vectorial de salida y el de llegada son el mismo). Automorfismo: Si es endomorfismo e isomorfismo a la vez.

Definición 1 Sean espacios vectoriales, y sea . Diremos que es:

Una transformación lineal (o morfismo ) si dados , ,

Un Monomorfismo si

es un morfismo inyectivo.
Un epimorfismo si

es un morfismo sobreyectivo.
Un isomorfismo si

es un morfismo biyectivo.

Además llamaremos ( para abreviar) al espacio de morfismos de $T : V \longrightarrow W$ , donde es la función constante cero, esto es:

$\displaystyle 0_{L} : V \longrightarrow W, \;\;\; 0_{L}(v) = 0_{w} \;\;\; (v \in V )$

Y la suma y producto escalar en se definen así:

Si $T, S \in L$ , entonces $T +_{L} S$ es la transformación dada por $( T +_{L} S )(v) = T(v) +_{W} S(v)$ .
Si , entonces es la transformación dada por.