En matemática una aplicación lineal (también llamada función lineal, transformación lineal u operador lineal) es una aplicación entre dos espacios vectoriales, que preserva las operaciones de suma de vectores y producto por un escalar.
En álgebra abstracta una aplicación lineal es un homomorfismo entre espacios vectoriales o en el lenguaje de la teoría de categorías un morfismo sobre la categoría de los espacios vectoriales sobre un
cuerpo dado.
Se denomina aplicación lineal, función lineal o transformación lineal a toda aplicación cuyo dominio y codominio sean espacios vectoriales que cumpla la siguiente definición:
- Sean
 y
y  espacios vectoriales sobre el mismo espacio o campo
espacios vectoriales sobre el mismo espacio o campo  , y
, y  una función de
una función de  en
en  .
.  es una transformación lineal si para todo par de vectores
es una transformación lineal si para todo par de vectores  y
y  pertenecientes a
pertenecientes a  y para todo escalar
y para todo escalar  perteneciente a
perteneciente a  , se satisface que:
, se satisface que:
-

 donde k es un escalar.
donde k es un escalar.
Transformación lineal identidad


Homotecias
 con
con 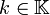
- Si k > 1 se denominan dilataciones
- Si k < 1 se denominan contracciones
- Sea B = {v1,v2,v3,...vn} base de V y C = {w1, w2, w3,...wn} un conjunto de n vectores de W no necesariamente distintos, entonces existe una única transformación lineal T: V → W que satisface:
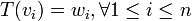
- Según la teoría de Brevis-Devaud, una matriz asociada es la matriz formada por las coordenadas de los elementos de una base.
Dada T: V → W, con B = {v1, v2, v3, ..., vn} y C = {w1, w2, w3, ..., wp} bases de V y W respectivamente, llamamos coordenadas de v1 en base C, al vector formado por los coeficientes de los elementos de C que usamos para llegar al transformado de v1.
T(v1) = a1.w1 + a2.w2 + ... + ap.wp
Entonces:
coordC(v1) = (a1, a2,..., ap)
Y la matriz asociada a T, en las bases B y C, es la matriz res/sub>(v2), ..., coordC(vn))
No hay comentarios:
Publicar un comentario