certidumbre: propiedades de las transformaciones lineales

lunes, 6 de agosto de 2012

propiedades de las transformaciones lineales

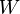Sean $V_{}^{}$ y $W_{}^{}$ espacios vectoriales sobre $K_{}^{}$ (donde $K_{}^{}$ representa el cuerpo) se satisface que:
Si 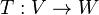$T: V \rarr W$ es lineal, se define el núcleo (ker) y la imagen (Im) de $T_{}^{}$ de la siguiente manera:

$\operatorname{ker}(T)=\{\,v\in V:T(v)=0_W\,\}$
$\operatorname{Im}(T)=\{\,w\in W: \exists v\in V:T(v)=w\,\}$

Es decir que el núcleo de una transformación lineal está formado por el conjunto de todos los vectores del dominio que tienen por imagen al vector nulo del codominio.
El núcleo de toda transformación lineal es un subespacio vectorial del dominio:

$0_V \in \operatorname{ker}(T)$ dado que $\operatorname {T}(0_V) = 0_W$
Dados $u , v \in \operatorname{ker}(T) : T(u+v) = T(u) + T(v) = 0_W + 0_W = 0_W \Rightarrow u + v \in \operatorname{ker}(T)$
Dados $u \in \operatorname{ker}(T) \and k \in \real : T(ku) = k T(u) \and T(ku) = k 0_W = 0_W \Rightarrow ku \in \operatorname{ker}(T)$

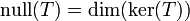
Se denomina nulidad a la dimensión del núcleo. $\operatorname{null}(T) = \operatorname{dim}(\operatorname{ker}(T))$
La imagen de una transformación lineal está formada por el conjunto de todos los vectores del codominio que son imágenes de al menos algún vector del dominio.

La imagen de toda transformación lineal es un subespacio del codominio.
El rango de una transformación lineal es la dimensión de la imagen.

$\operatorname{ran}(T) = \operatorname{dim}(\operatorname{Im}(T))$

una función lineal es la correspondencia

certidumbre

lunes, 6 de agosto de 2012

propiedades de las transformaciones lineales

No hay comentarios:

Publicar un comentario