certidumbre: TRANSFORMACION INVERSA

Sea X una variable aleatoria con función de distribución F_X(x).

Por resultados básicos de probabilidad, se tiene que U=F_X(X) es una variables aleatoria y sigue una distribución U(0,1). A continuación veremos un resultado recíproco. Previamente, establecemos la siguiente notación: dado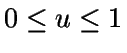 $0\leq u \leq 1$ , se define

$\begin{displaymath}F_X^{-1}(u) = \min \{y \ / \ F_X(y)\geq u \}.\end{displaymath}$

Si $U\equiv U(0,1)$ y F es una función de distribución, entonces X=F^-1(U) tiene función de distribución F.
Demostración:
(i) Nótese en primer lugar que

$\begin{displaymath}F(F^{-1}(u)) = F( \text{mín} \{y \ / \ F(y) \geq u \} ) \geq u,\end{displaymath}$

$\begin{displaymath}F^{-1}(F(x))=\text{mín} \{y \ / \ F(y) \geq F(x) \} \leq x.\end{displaymath}$

(ii) Veamos que $\{ (u,x) \ / \ u\leq F(x)\}=\{(u,x) \ / \ F^{-1}(u) \leq x \}$ .
" $\subseteq$ " Sea (u,x) un elemento del primer conjunto.

$\begin{displaymath}u \leq F(x) \quad \rightarrow \quad F^{-1}(u)=\text{mín} \{y \ / \ F(y) \geq u \} \leq x .\end{displaymath}$

Luego (u,x) está en el segundo conjunto.

" $\supseteq$ " Sea ahora (u,x) un elemento del segundo conjunto.

$\begin{displaymath}F^{-1}(u) \leq x \quad \rightarrow \quad u \leq F(F^{-1}(u)) \leq F(x).\end{displaymath}$

Por lo tanto, (u,x) pertenece al primer conjunto.

(iii)

$\begin{displaymath}P(X\leq x) = P(F^{-1}(U)\leq x) = P(\{ (u,x) \ / \ F^{-1}(u)\leq x \}) =\end{displaymath}$

$\begin{displaymath}P(\{ (u,x) \ / \ u\leq F(x)\}) = P(U\leq F(x)) = F(x).\end{displaymath}$

La última igualdad por tratarse de una variable uniforme en el intervalo (0,1).

Q.E.D.

Así se tiene el siguiente método de la transformación inversa:

1.: Genérese u_i.
2.: Hágase x_i=F_X^-1(u_i).

Ejemplo: $X\equiv U(a,b)$

$\begin{displaymath}F_X(x)= \frac {x-a}{b-a}, \ x\in (a,b)\end{displaymath}$

$\begin{displaymath}\frac{x-a}{b-a}=u; \quad x-a=u(b-a); \quad x=a+(b-a)u\end{displaymath}$

Ejemplo: $X\equiv Exp(\lambda)$

$\begin{displaymath}F_X(x)=1-e^{-\lambda x}, \ x>0\end{displaymath}$

$\begin{displaymath}1-e^{-\lambda x} = u; \quad 1-u=e^{-\lambda x}; \quad x= - \frac{1}{\lambda} \ln (1-u).\end{displaymath}$

Ejemplo: $X_1,\dots,\ X_n$ variables aleatorias independientes con la misma función de distribución F_X y

$\begin{displaymath}X_{(n)}=\text{máx} \{X_1,\dots,\ X_n\}.\end{displaymath}$

$\begin{displaymath}F_{(n)}(x)=P(X_{(n)}\leq x)=P(X_1\leq x,\dots,\ X_n\leq x)= \end{displaymath}$

$\begin{displaymath}=\prod_{i=1}^n P(X_i\leq x) = F_X^n(x).\end{displaymath}$

$\begin{displaymath}F_X^n(x)=u\Rightarrow \quad x=F_X^{-1}(u^{\frac{1}{n}}).\end{displaymath}$

Sin embargo, este método presenta problemas cuando no es posible obtener F_X^-1 de forma explícita (por ejemplo, en la distribución normal).

certidumbre

martes, 7 de agosto de 2012

TRANSFORMACION INVERSA

No hay comentarios:

Publicar un comentario