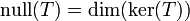Cualquier conjunto de n números reales que verifica la ecuación se denomina solución de la ecuación.
Dada la ecuación x + y + z + t = 0, son soluciones de ella:
(1,-1,1,-1), (-2,-2,0, 4).
Es un conjunto de expresiones algebraicas de la forma:
a11x1 + a12x2 + .....................+a1nxn = b1
a21x1 + a22x2 + .....................+a2nxn = b2
...............................................................
am1x1 + am2x2 + .....................+amnxn = bm
- xi son las incógnitas, (i = 1,2,...,n).
-
aij son los coeficientes, (i = 1,2,...,m) (j = 1,2,...,n).
- bi son los términos independientes, (i = 1,2,...,m).
-
m, n

 ; m > n, ó, m = n, ó, m < n.
; m > n, ó, m = n, ó, m < n.
-
Obsérvese que el número de ecuaciones no tiene por qué ser igual al número de incógnitas.
- aij y b i

 .
.
-
Cuando n toma un valor bajo, es usual designar a las incógnitas con las letras x, y, z, t, ...
- Cuando bi = 0 para todo i, el sistema se llama homogéneo.
Las ecuaciones lineales o de primer grado son del tipo ax + b = 0 , con a ≠ 0, ó cualquier otra ecuación en la que al operar, trasponer términos y simplificar adopten esa expresión.
Resolución de ecuaciones lineales
En general para resolver una ecuación lineal o de primer grado debemos seguir los siguientes pasos:
1º Quitar paréntesis.
2º Quitar denominadores.
3º Agrupar los términos en x en un miembro y los términos independientes en el otro.
4º Reducir los términos semejantes.
5º Despejar la incógnita.
Ejemplos de ecuaciones lineales
Despejamos la incógnita:
Agrupamos los términos semejantes y los independientes, y sumamos:
Quitamos paréntesis:
Agrupamos términos y sumamos:
Despejamos la incógnita:
Quitamos denominadores, para ello en primer lugar hallamos el mínimo común múltiplo.
Quitamos paréntesis, agrupamos y sumamos los términos semejantes:
Despejamos la incógnita:
Quitamos paréntesis y simplificamos:
Quitamos denominadores, agrupamos y sumamos los términos semejantes:
Quitamos corchete:
Quitamos paréntesis:
Quitamos denominadores:
Quitamos paréntesis:
Agrupamos términos:
Sumamos:
Dividimos los dos miembros por: −9
 y
y 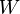 espacios vectoriales sobre
espacios vectoriales sobre  (donde
(donde  representa el cuerpo) se satisface que:
representa el cuerpo) se satisface que: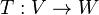 es lineal, se define el núcleo (ker) y la imagen (Im) de
es lineal, se define el núcleo (ker) y la imagen (Im) de  de la siguiente manera:
de la siguiente manera: dado que
dado que